Hoe Breuken Vermenigvuldigen: Tips Voor Succes
Table of Contents
Breuken Vermenigvuldigen-Deel 1 – Wiskundeacademie
Keywords searched by users: hoe breuken vermenigvuldigen breuken rekenmachine, gemengde breuken vermenigvuldigen, breuken delen, breuk vermenigvuldigen met getal, breuken vermenigvuldigen rekenmachine, breuken vermenigvuldigen oefenen, breuken vermenigvuldigen met breuken, breuken vermenigvuldigen en delen
Wat zijn breuken?
Breuken zijn een fundamenteel concept in de wiskunde en juist begrip van hoe ze werken is essentieel voor vele aspecten van het dagelijks leven. Een breuk kan worden gezien als een deel van een geheel. Het bestaat uit een teller en een noemer, gescheiden door een streep.
De teller vertegenwoordigt het aantal delen dat we hebben, terwijl de noemer het totale aantal delen in een geheel vertegenwoordigt. Bijvoorbeeld, in de breuk 3/4, is 3 de teller en 4 de noemer. Dit betekent dat we 3 delen hebben van een geheel dat is verdeeld in 4 gelijke delen.
Het begrip breuken is van toepassing op vele situaties, zoals het verdelen van een pizza in gelijke stukken, het berekenen van percentages, het meten van ingrediënten bij het koken, het berekenen van snelheid en nog veel meer.
Hoe vermenigvuldig je breuken met elkaar?
Het vermenigvuldigen van breuken is een eenvoudig proces dat kan worden uitgevoerd door de tellers met elkaar te vermenigvuldigen en vervolgens de noemers met elkaar te vermenigvuldigen. Het resulterende product is de vermenigvuldiging van de twee breuken.
Laten we dit illustreren aan de hand van een voorbeeld. Laten we zeggen dat we de breuken 2/3 en 3/5 willen vermenigvuldigen. We vermenigvuldigen eerst de tellers (2 x 3 = 6) en vervolgens de noemers (3 x 5 = 15). Het resultaat is de breuk 6/15.
Om de breuk te vereenvoudigen, kunnen we de grootste gemene deler (GGD) van de teller en de noemer berekenen en de breuk delen door de GGD. In dit geval is de GGD van 6 en 15 gelijk aan 3. Als we de breuk 6/15 delen door 3, krijgen we de vereenvoudigde breuk 2/5.
Dus, om breuken met elkaar te vermenigvuldigen, vermenigvuldigen we de tellers en vermenigvuldigen we de noemers. Daarna kunnen we de breuk vereenvoudigen indien nodig.
Vermenigvuldigen van twee breuken
Om twee breuken met elkaar te vermenigvuldigen, moeten we de tellers met elkaar vermenigvuldigen en vervolgens de noemers met elkaar vermenigvuldigen. Het resulterende product is de vermenigvuldiging van de twee breuken.
Laten we dit demonstreren met een voorbeeld. Stel dat we de breuken 2/3 en 4/5 willen vermenigvuldigen. We vermenigvuldigen de tellers (2 x 4 = 8) en vervolgens de noemers (3 x 5 = 15). Het resultaat is de breuk 8/15.
We kunnen de breuk vervolgens vereenvoudigen door de grootste gemene deler (GGD) van de teller en de noemer te berekenen en de breuk te delen door de GGD. In dit geval is de GGD van 8 en 15 gelijk aan 1. Als we de breuk 8/15 delen door 1, krijgen we dezelfde breuk 8/15.
Vermenigvuldigen van een breuk en een heel getal
Het vermenigvuldigen van een breuk en een heel getal volgt een vergelijkbaar proces. We vermenigvuldigen gewoon de teller van de breuk met het hele getal en behouden de noemer hetzelfde.
Laten we dit uitleggen aan de hand van een voorbeeld. Stel dat we de breuk 3/4 willen vermenigvuldigen met het hele getal 2. We vermenigvuldigen de teller (3 x 2 = 6) en behouden de noemer hetzelfde. Het resultaat is de breuk 6/4.
Merk op dat deze breuk kan worden vereenvoudigd. De grootste gemene deler (GGD) van 6 en 4 is 2. Als we de breuk 6/4 delen door 2, krijgen we de vereenvoudigde breuk 3/2.
Vermenigvuldigen van een breuk en een gemengd getal
Om een breuk te vermenigvuldigen met een gemengd getal, moeten we het gemengde getal converteren naar een onechte breuk en het vervolgens vermenigvuldigen zoals we dat met twee breuken zouden doen.
Laten we dit begrijpen door middel van een voorbeeld. Stel dat we de breuk 1/3 willen vermenigvuldigen met het gemengde getal 2 1/4. Ten eerste converteren we het gemengde getal naar een onechte breuk. Dit kan worden gedaan door de gehele getallen te vermenigvuldigen met de noemer van de breuk en het resultaat op te tellen bij de teller. In dit geval is de onechte breuk gelijk aan (2 x 4 + 1) / 4 = 9/4.
Vervolgens vermenigvuldigen we de twee breuken 1/3 en 9/4 door de tellers met elkaar te vermenigvuldigen en de noemers met elkaar te vermenigvuldigen. Het product is gelijk aan (1 x 9) / (3 x 4) = 9/12.
We kunnen deze breuk vervolgens vereenvoudigen door de grootste gemene deler (GGD) van de teller en de noemer te berekenen en de breuk te delen door de GGD. In dit geval is de GGD van 9 en 12 gelijk aan 3. Als we de breuk 9/12 delen door 3, krijgen we de vereenvoudigde breuk 3/4.
Vermenigvuldigen van breuken met ongelijke noemers
Als we breuken met ongelijke noemers willen vermenigvuldigen, moeten we ze eerst gelijknamig maken voordat we ze met elkaar kunnen vermenigvuldigen. Dit betekent dat we de noemers van de breuken gelijk moeten maken voordat we de vermenigvuldiging kunnen uitvoeren.
Laten we dit verduidelijken met een voorbeeld. Stel dat we de breuken 1/2 en 2/3 willen vermenigvuldigen. Om de noemers gelijk te maken, moeten we de breuken vermenigvuldigen met de ontbrekende factor in de noemer van de andere breuk. In dit geval moeten we de eerste breuk vermenigvuldigen met 3 en de tweede breuk vermenigvuldigen met 2.
De nieuwe breuken zijn dan 3/6 en 4/6. Nu kunnen we de vermenigvuldiging uitvoeren door de tellers met elkaar te vermenigvuldigen en de noemers met elkaar te vermenigvuldigen. Het resultaat is de breuk (3 x 4) / (6 x 6) = 12/36.
Deze breuk kan worden vereenvoudigd door de grootste gemene deler (GGD) van de teller en de noemer te berekenen en de breuk te delen door de GGD. In dit geval is de GGD van 12 en 36 gelijk aan 12. Als we de breuk 12/36 delen door 12, krijgen we de vereenvoudigde breuk 1/3.
Vermenigvuldigen van breuken met gelijke noemers
Als beide breuken dezelfde noemer hebben, hoeven we geen extra stappen te nemen om de vermenigvuldiging uit te voeren. We vermenigvuldigen gewoon de tellers met elkaar en behouden de noemer hetzelfde.
Laten we dit demonstreren met een voorbeeld. Stel dat we de breuken 2/5 en 3/5 willen vermenigvuldigen. Omdat de noemers gelijk zijn, vermenigvuldigen we de tellers (2 x 3 = 6) en behouden we de noemer hetzelfde. Het resultaat is de breuk 6/5.
Deze breuk kan mogelijk worden vereenvoudigd. De grootste gemene deler (GGD) van 6 en 5 is 1. Als we de breuk 6/5 delen door 1, blijft de breuk hetzelfde, 6/5.
Vermenigvuldigen van breuken met negatieve getallen
Het vermenigvuldigen van breuken met negatieve getallen werkt op dezelfde manier als het vermenigvuldigen van breuken met positieve getallen. We vermenigvuldigen gewoon de tellers met elkaar en de noemers met elkaar. Het enige verschil is dat het resulterende product negatief zal zijn als een van de breuken negatief is.
Laten we dit illustreren met een voorbeeld. Stel dat we de breuken 2/3 en -1/4 willen vermenigvuldigen. We vermenigvuldigen de tellers (2 x -1 = -2) en de noemers (3 x 4 = 12). Het resulterende product is de breuk -2/12.
Deze breuk kan worden vereenvoudigd door de grootste gemene deler (GGD) van de teller en de noemer te berekenen en de breuk te delen door de GGD. In dit geval is de GGD van -2 en 12 gelijk aan 2. Als we de breuk -2/12 delen door 2, krijgen we de vereenvoudigde breuk -1/6.
Vermenigvuldigen van breuken met nul
Als een van de breuken gelijk is aan nul, zal het resultaat van de vermenigvuldiging altijd nul zijn. Dit komt doordat nul vermenigvuldigd met een willekeurig getal altijd nul oplevert.
Laten we dit verduidelijken met een voorbeeld. Stel dat we de breuken 0/3 en 2/5 willen vermenigvuldigen. Omdat een van de breuken gelijk is aan nul (0/3), zal het resultaat van de vermenigvuldiging altijd nul zijn, ongeacht de waarde van de andere breuk.
Het product is dus gelijk aan 0. Dit betekent dat als een van de breuken gelijk is aan nul, het resultaat van de vermenigvuldiging altijd nul zal zijn.
Praktijkvoorbeelden en oefeningen voor het vermenigvuldigen van breuken
Om uw begrip van het vermenigvuldigen van breuken te versterken, kunt u de volgende praktijkvoorbeelden en oefeningen uitproberen:
1. Bereken de vermenigvuldiging van de breuken 2/3 en 4/5.
2. Vermenigvuldig de breuk 3/4 met het hele getal 2.
3. Bereken het product van de breuk 1/5 en het gemengde getal 3 2/7.
4. Vermenigvuldig de breuk 2/7 met het negatieve getal -3.
5. Wat
Categories: Verzamelen 100 Hoe Breuken Vermenigvuldigen

Bij het vermenigvuldigen van breuken moeten de tellers met elkaar worden vermenigvuldigd en de noemers met elkaar worden vermenigvuldigd. Ook bij het delen van breuken hoeven de noemers niet hetzelfde te zijn. Voor delen geldt: delen door een breuk is vermenigvuldigen met het omgekeerde (van die breuk).Als je heel getal wilt vermenigvuldigen met een breuk, dan kun je dat hele getal vermenigvuldigen met de teller van die breuk. Dit komt omdat je een getal ook als breuk kunt opschrijven. Het is gelijk aan dat hele getal gedeeld door één. Dus 7 = 7/1.Maak de breuken gelijknamig, oftewel zorg dat alle breuken dezelfde noemer hebben. Ga hiervoor opzoek naar het kleinste gemeenschappelijke veelvoud (kgv) van de noemers. Tel de tellers bij elkaar op of trek de tellers van elkaar af. Haal de helen uit de uitkomst en vereenvoudig de breuk als dit mogelijk is.
- de teller x de teller (onthoud: de teller is het cijfer boven de breukstreep) te doen en.
- de noemer x de noemer (onthoud: de noemer is het cijfer onder de breukstreep) te doen.
- Een getal delen door een breuk is hetzelfde als het getal vermenigvuldigen met het omgekeerde van de breuk.
- Een breuk delen door een breuk is hetzelfde als de breuk vermenigvuldigen met het omgekeerde van de breuk.
Hoe Breuken Vermenigvuldigen Met Een Natuurlijk Getal?
Hoe Moet Je Ongelijknamige Breuken Vermenigvuldigen?
Om ongelijknamige breuken met elkaar te vermenigvuldigen, vermenigvuldig je de teller (het cijfer boven de breukstreep) met de andere teller en de noemer (het cijfer onder de breukstreep) met de andere noemer. Onthoud dat de teller x teller en de noemer x noemer zijn.
Hoe Moet Je 3 Breuken Bij Elkaar Optellen?
Om 3 breuken bij elkaar op te tellen, moeten de breuken gelijknamig gemaakt worden, dit betekent dat alle breuken dezelfde noemer moeten hebben. Om dit te bereiken, moet je op zoek gaan naar het kleinste gemeenschappelijke veelvoud (kgv) van de noemers. Nadat de breuken gelijknamig zijn gemaakt, tel je de tellers bij elkaar op of trek je de tellers van elkaar af. Als er hele getallen voorkomen in de uitkomst, haal dan deze getallen eruit en vereenvoudig de breuk indien mogelijk.
Hoe Moet Je Een Breuk Delen?
Vuistregels voor het delen van breuken:
1. Om een getal te delen door een breuk, vermenigvuldig je het getal met het omgekeerde van de breuk. Dit betekent dat je de breuk omdraait, zodat de teller de noemer wordt en andersom, en vervolgens deze omgedraaide breuk vermenigvuldigt met het getal.
2. Om een breuk te delen door een breuk, vermenigvuldig je de eerste breuk met het omgekeerde van de tweede breuk. Ook hier draai je de tweede breuk om en vermenigvuldig je de eerste breuk met deze omgedraaide breuk.
Hoe Bereken Je Twee Breuken?
Om twee breuken te delen, vermenigvuldig je de eerste breuk met het omgekeerde van de tweede breuk. Om het omgekeerde van de tweede breuk te vinden, wissel je de teller en de noemer om. Vervolgens vermenigvuldig je de twee tellers.
Delen 10 hoe breuken vermenigvuldigen



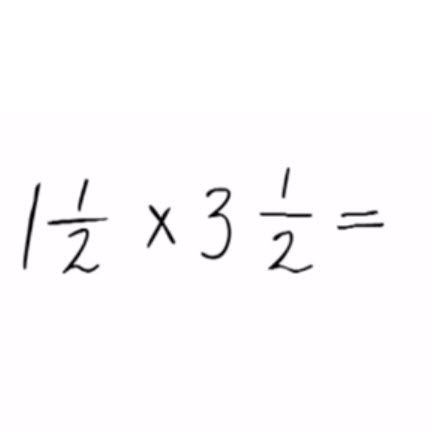


See more here: brokengroundgame.com
Learn more about the topic hoe breuken vermenigvuldigen.
- Breuken optellen, aftrekken, vermenigvuldigen en delen
- 28 | Vermenigvuldigen van een breuk en een heel getal
- Ongelijknamige breuken met elkaar vermenigvuldigen (open) – Slimleren
- Breuken optellen en aftrekken – Slimleren
- Breuken delen – Slimleren
- Breuken delen: 3/5 ÷ 1/2 (video) – Khan Academy
See more: https://brokengroundgame.com/music/

